General purpose optimization
Z-opt is a general purpose optimization package that can be interfaced with any external software communicating by ASCII input files, or any other solution. The package is specially designed as a tool for material parameter identification, where the optimal parameter set minimizes a functional defining the distance between the experimentally observed response and the simulation.
The Z-opt input file is very flexible. The experimental data can originate from any kind of simple test (tensile, creep, one-dimensional or multiaxial), or from hybrid data bases on material elements and structures: Z-opt can drive any external software to compute the simulated data and solve any kind of parameterized problem. For example, it can be used to optimize the friction coefficient, to determine convection parameters in thermal computations, or to perform shape optimization.
Given an initial set of parameters, Z-opt computes the least-square distance between experiments (stored in data files) and simulations (obtained with Z-sim, or any other computation software). The optimization algorithm provides an updated set of parameters using the method selected by the user (heuristic or gradient driven), which replaces the previous one. The optimization loop ends once the optimal set of parameters is reached.
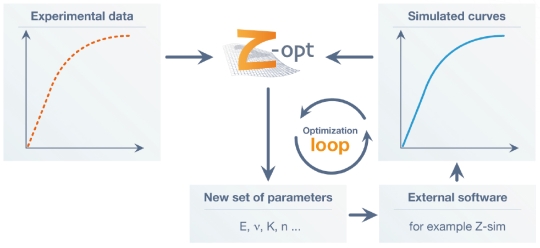
External software is not required if the simulated curve can be defined by an analytical function: in this case, Z-opt computes this function and performs the optimization internally. Several optimization methods are available in the package, accounting for its versatility over a wide range of optimization problems:
- two gradient-driven methods: Levenberg-Marquardt, which is particularly efficient for least-square type of cost-functions, and SQP, a more general state-of-the-art algorithm accepting optimization under constraint
- simplex, a heuristic local method that does not need any gradient analysis and is very efficient on strongly non-linear problems
- genetic algorithm, which can bypass local minima in the case of non-convex problems. It is insensitive to the starting point and provides a whole family of possible solutions.