Non-linear finite element solver
Zébulon is the state-of-the-art finite element solver of the Z-set suite. It addresses the entire range of problems arising in structural mechanics. From the very beginning, the code has specialized in highly non-linear material models and has since evolved to include thermal and diffusion problems and to handle the coupling of those models.
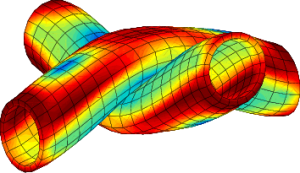
Material non-linearity
Material models are natively managed by Z-mat: they range from simple isotropic elasticity to anisotropic elasto-viscoplasticity through complex polymer behaviors, damageable composites and even multiscale models. Non-linearities arising from material models, finite transformations or contact friction are handled by a complete set of solvers, offering full control of both physical and numerical convergence parameters.
Thermal, diffusion and coupled problems
A thermal analysis module solves steady state and transient thermal problems; multiphase Fick’s diffusion problems are handled as well. In fact, any other type of elliptic or parabolic problems can be addressed similarly. A weak coupling module handles an arbitrary number of such problems (e.g., thermo-mechanical-diffusion analysis). To deal with more complex multi-physics models, Zébulon also comes with external coupling capabilities, with fluid flow or radiation software packages for instance.
Crack simulation
Crack propagation is carried out by the Z-cracks module. With both remeshing techniques and SIF estimation strategies, Z-cracks is a very robust and efficient tool for fatigue or brittle crack propagation problems.
Static, dynamic and modal analysis
Zébulon’s implicit solver handles static or transient dynamic problems.
Using one of its eigen-mode solvers, a modal analysis can also be performed.
High performance computing
High performance computing strategies are used on recent SMP processors and clusters, through a 2-level parallelization approach:
– on a single shared memory machine, multi-threading is used to accelerate both material integration and linear system resolution;
– on distributed memory cluster architectures, the domain decomposition technique is implemented.
User additions
Two methods are available for extending the code capabilities: Z-program or a plug-in mechanism.
Z-program is a complete interpreted scripting language based on C++ and that allows interaction with the main internal objects of Z-set. An unlimited number of user extensions can be handled within the Object Oriented architecture by using the derivation/plug-in mechanism. Specific boundary conditions, new element formulations, post-increment procedures, post-processing computations and many other features can be developed and linked to the main code in this way.
Element library
General purpose elements:
- 2D elements: linear and quadratic triangles and quadrangles
- 3D elements: linear and quadratic tetrahedra, hexahedra, prisms and pyramids
- 1D and 1.5D elements
- Structural elements: shells, beams and trusses
- Layered elements for composite laminates
- Interface elements with cohesive zone models
Specialized elements:
- Periodic elements
- Bubble-elements (pressure-displacement formulation) for incompressible materials
- Non-local and micro-morph elements
Element formulations:
- Plane stress, plane strain and axisymmetric formulations
- Small or finite strain formulations
- 2.5D for generalized plane strain formulations
- Cosserat continuum models with 2nd grade continuum
- Micromorphic formulations
Resolution algorithms
- Quasi-Newton with optional BFGS
- Arc-length algorithm for buckling and more general softening behavior
- Time-stepping control automatically adjusted to material state variable evolution or global Newton iterations
- Implicit generalized midpoint integration method (θ-method) and explicit Runge-Kutta integration scheme, with automatic control of local time-stepping
- Direct and iterative state-of-the-art linear solvers
High performance computing
- Multithreading of material integration
- Multithreading of linear system resolution
- Parallelization through domain decomposition: BDD, FETI-DP and FETI-2LM
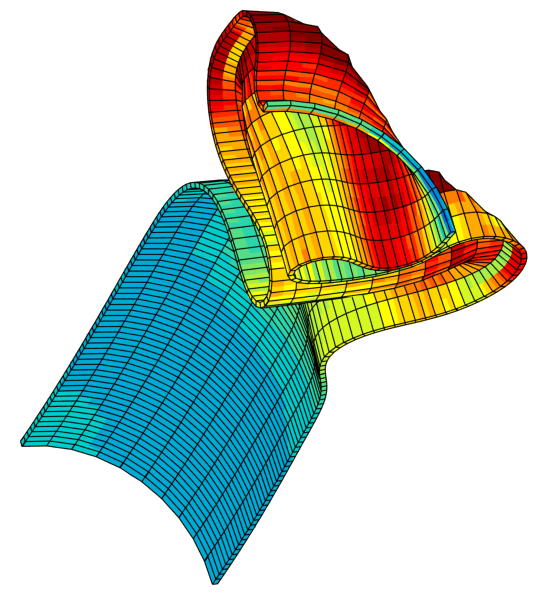
Model reduction
- Innovative techniques for accelerating non-linear problem resolution
- Hyper reduction
Acceleration methods
- Skip cycle method
- Explicit methods to reach the stabilized cycle
Remeshing/Crack propagation
- 2D/3D adaptative mesh refinement
- Various field transfer methods
- Stress Intensity Factor computing by G-θ method coupled to various crack propagation models
- Automatic crack insertion and propagation (planar and non-planar)
Multiscale and multiphysics analysis
- FE² for multiscale FE analysis: behavior at each macro-scale integration point is defined by a micro-scale FE problem
- Submodeling
- Arlequin patch methods
- Code coupling, both internally with other Zébulon instances, or with other software for fluid-structure simulations
Homogenization
- Special boundary conditions
- Periodic element
External parameters
- Unlimited number of external parameters – uniform and non-uniform
- Import and transfer of external parameters from preliminary computations