Z-set provides numerous tools to model the mechanical processes specific to composite material deformation and degradation.
Mixed mode delamination under complex loads
Crisfield, Tvergaard and Chaboche type cohesive zone models are available in Z-set, to simulate mixed mode delamination in composite laminate structures under complex combined tensile, compressive and flexural loads. The mode mixity, and thus the delamination behavior, evolves with changes in the load conditions throughout the simulation.
The Z-mat material library includes constitutive models for composite materials, specifically designed to take into account their high anisotropy. Material orientation can be easily entered for each ply of the laminate. Large displacement algorithms correctly follow the orientation of the principal axes of the material during structural deformation, such as rotation, flexion or buckling, which ensures correct load transfer at any time of the simulation.
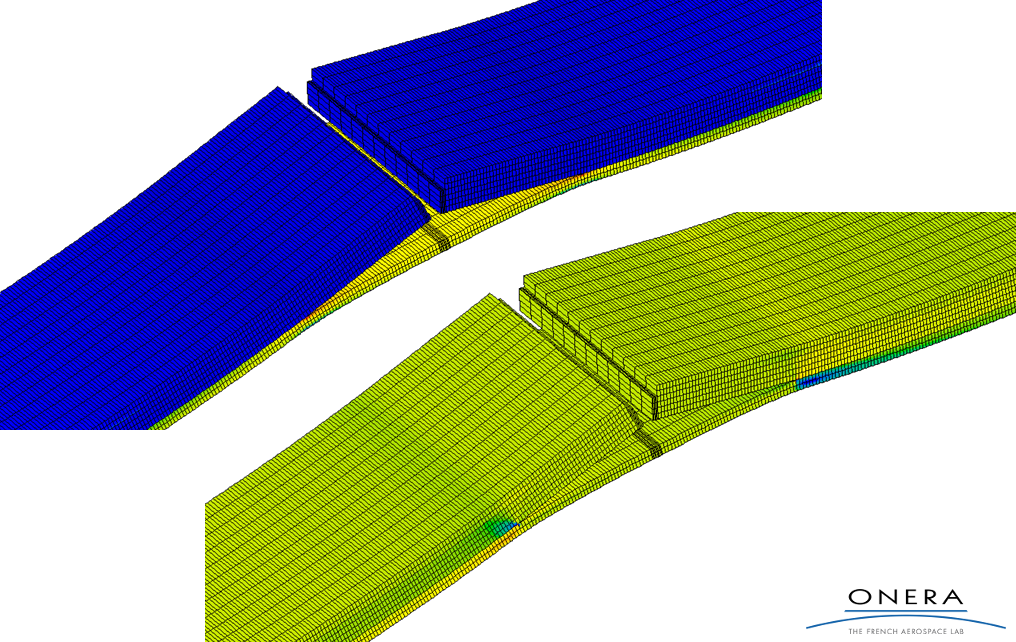
Modeling of a tensile flexure test on a notched laminate specimen with mixed mode I/II delamination between the plies [1] (Axial and shear stress on display)

Crack density and interface damage of a [45m°/90m°/-45m°/0m°]s IM7/8552 open-hole plate at tensile failure [2].
Coupled modeling of ply damage and delamination to predict composite failure stress levels and failure modes
The material library includes damage models specifically developed for different types of composite materials (laminates, textile composites, metal composites, etc.). These models take into account the different damage modes (fiber fracture, fiber-matrix decohesion, fiber kinking, matrix fracture, etc.), and the local failure mode can be displayed in post-processing. Coupling between failure modes (e.g. delamination and ply failure in composite laminates) are taken into account. Regularization algorithms are available to tackle numerical issues arising from damage localization and geometrical singularity.
Multi-scale modeling of composite materials
Z-set provides a wide range of boundary conditions, with a particularly comfortable application of periodic boundary conditions for numerical homogenization of composite properties. Finite Element simulations provide local stress and strain fields at the micro-scale. The macro-scale average behavior can be computed by post-processing algorithms.
Complex fiber orientation distributions that change continuously in space can be entered easily by means of Python or Z-language scripts, offering a high flexibility in the numerical simulation of advanced composite materials with complex fiber reinforcement architectures (e.g., textile composites).
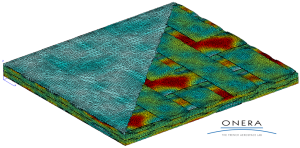
Transverse stress distribution in a 4-layer nested 5-harness satin composite layup under tension in the warp yarn direction [3].