**strain_gradient

Description

This boundary condition applies displacement over a valid node set, such as

\[\vect u=\ten E \cdot \vect y +\dfrac{1}{2}\tent D :\left(\vect y \otimes \vect y\right) \qquad \forall \vect y \in \boldsymbol{\Omega}\]

where \(\tent D\) is the strain gradient third-rank tensor and \(\ten E\) is a symmetric strain tensor. The strain gradient tensor \(\tent D\) is defined as the second derivative of the displacement vector \(\vect u\):

\[D_{ijk} = u_{i,jk}\]

It has 18 indepedent components since \(u_{i,jk}=u_{i,kj}\).

Syntax

**strain_gradient \(~\,~\,\) nset  (origin)  strain|strain_grad value  table

where

nset

is the nset on which the boundary condition is applied.

origin

is the origin vector w.r.t which the vector position \(\vect y\) is computed.

strain/strain_grad

is the strain or strain gradient to be applied.

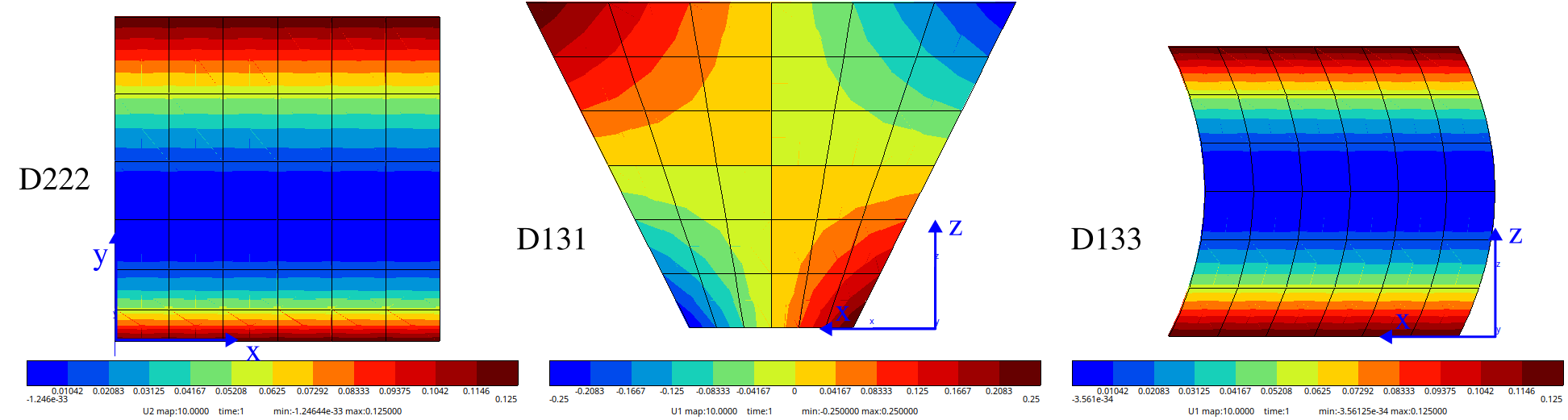
Strain	E11, E11, E22, E12, [ E33, E23, E31 ]
Strain gradient	D111, D122, D112, D211, D222, D212, [ D223, D231, D311, D322, D333, D312, D323, D331, D133, D233, D131, D123 ]

value

is the value to be applied (multiplied by table).

Example

***bc
  **strain_gradient
    ALL_NODE ( 0.500000 0.500000 0.500000 ) D222  1.00000 tab