memory

Description

This behavior is a ZebFront implementation of a strain range memory isotropic hardening model described by Lemaitre and Chaboche [M8]. The model has 2 non-linear kinematic hardening components (coefficients C1, D1, C2, and D2), and a Norton type flow law (coefficients K and n).

The yield criterion is given by

\[f=J(\ten \sigma-\ten X_1-\ten X_2)-R\]

where \(J(\diamond) = \sqrt{\dfrac{3}{2}\diamond^{dev}:\diamond^{dev}}\), and \(\diamond^{dev}\) is the deviatoric part.

The viscoplastic flow rule is

\[\dot{p}=\dfrac{<f>}{\tt K}^{\tt n}\]

The constitutive equations are:

\[\begin{split}\begin{aligned} \ten \sigma &= \tenf{\mathbb{C}}:\ten \varepsilon^e\\ \ten X_1 &= \dfrac{2}{3} {\tt C1} \ten \alpha_1 \\ \ten X_2 &= \dfrac{2}{3} {\tt C2} \ten \alpha_2 \\ R &= {\tt R0} + Q(1-e^{-{\tt b}p}) \end{aligned}\end{split}\]

where \(\tenf{\mathbb{C}}\) is the elasticity fourth-rank tensor. The evolution equations for kinematic hardening internal variables are

\[\begin{split}\begin{aligned} \dot{\ten \alpha}_1 &= \dot{p}\left(\ten n-{\tt D1}\ten\alpha_1\right)\\ \dot{\ten \alpha}_2 &= \dot{p}\left(\ten n-{\tt D2}\ten\alpha_2\right) \end{aligned}\end{split}\]

where \(\ten n=\dfrac{3}{2}\dfrac{\ten \sigma^{dev}-\ten X_1-\ten X_2}{J(\ten \sigma-\ten X_1-\ten X_2)}\) is the normal to the loading surface \(f=0\).

As observed for 316L stainless steel [M8], the asymptotic value of the cyclic hardening (\(Q\)) may depend on the strain amplitude. Two additional variables are added to keep track of the plastic strain range: the center \(\ten{\xi}\) and the radius \(q\) of the plastic strain enveloping surface \(F\),

\[F = \dfrac{2}{3}J(\ten \varepsilon^p-\xi)-q\]

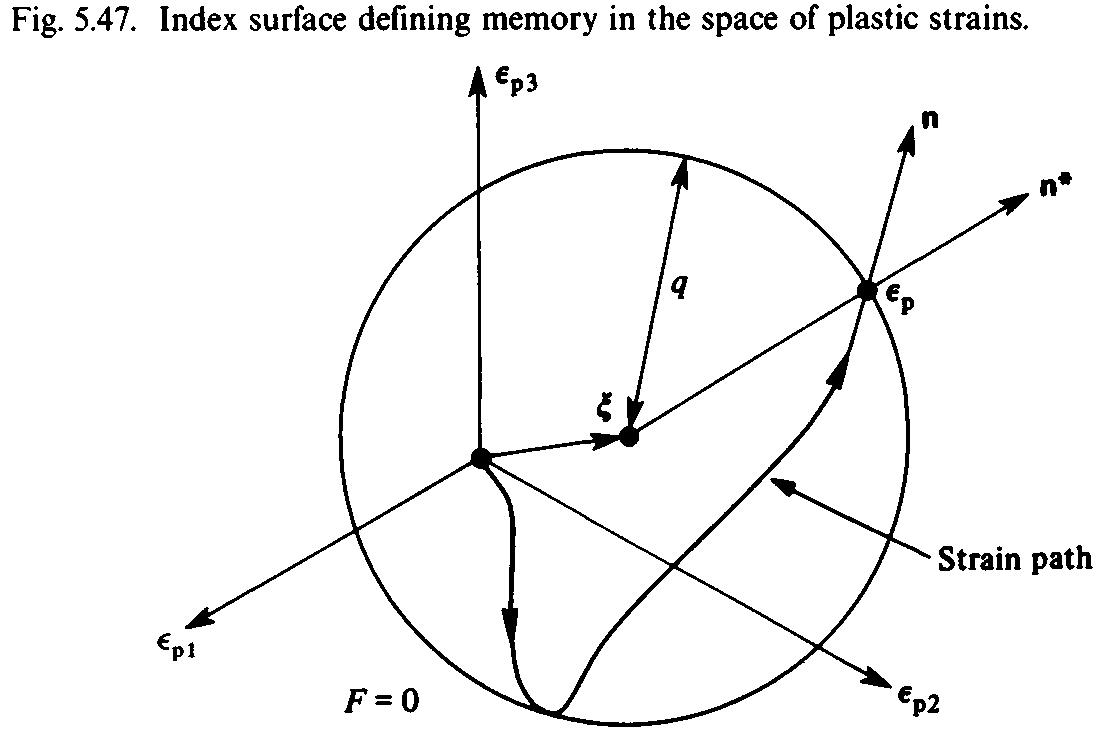
The enveloping surface of previous strains will move only when the current strain state is on the surface \(F=0\), and that the flow occurs in the direction external to the surface. The evolution equations are given by:

\[\begin{split}\begin{aligned} \dot{\ten \xi} &= \dfrac{1}{2} (\ten n^*:\ten \varepsilon^{p})\ten n^* H(F)\\ \dot{q} &= \eta \dot{p} H(F) \end{aligned}\end{split}\]

where \(H(x)=1\) if \(x\geq 0\), \(H(x)=0\) if \(x<0\). The variable \(\eta\) is determined by the consistency condition \(dF=0\):

\[\eta = \dfrac{\ten n:\ten n^*}{2 |\ten n:\ten n^*|}\]

where \(\ten n^*\) is the normal to the index surface \(F = 0\):

\[\ten n^* = \sqrt{\dfrac{3}{2}}\dfrac{\ten \varepsilon^p - \ten \xi}{J(\ten \varepsilon^p - \ten \xi)}\]

The asymptotic value \(Q_{sat}\) of isotropic hardening depends on the variable \(q\) as:

\[Q = {\tt Q_{sat}} - ({\tt Q_{sat}}-{\tt Q0}) \exp(-2 {\tt mu}~q)\]

Syntax

***behavior memory \(~\,\) **elasticity <ELASTICITY> \(~\,\) **model_coef \(~\,~\,~\,\) coefs

Example

***behavior memory
 **elasticity isotropic
   young 200000.
   poisson 0.3
 **model_coef
   n     5.
   K     50.
   C1    1000.0
   D1    20.
   C2    12000.
   D2    120.
   R0    50.
   b     25.
   Q0    25.
   Qsat  400.
   mu    50.
***return

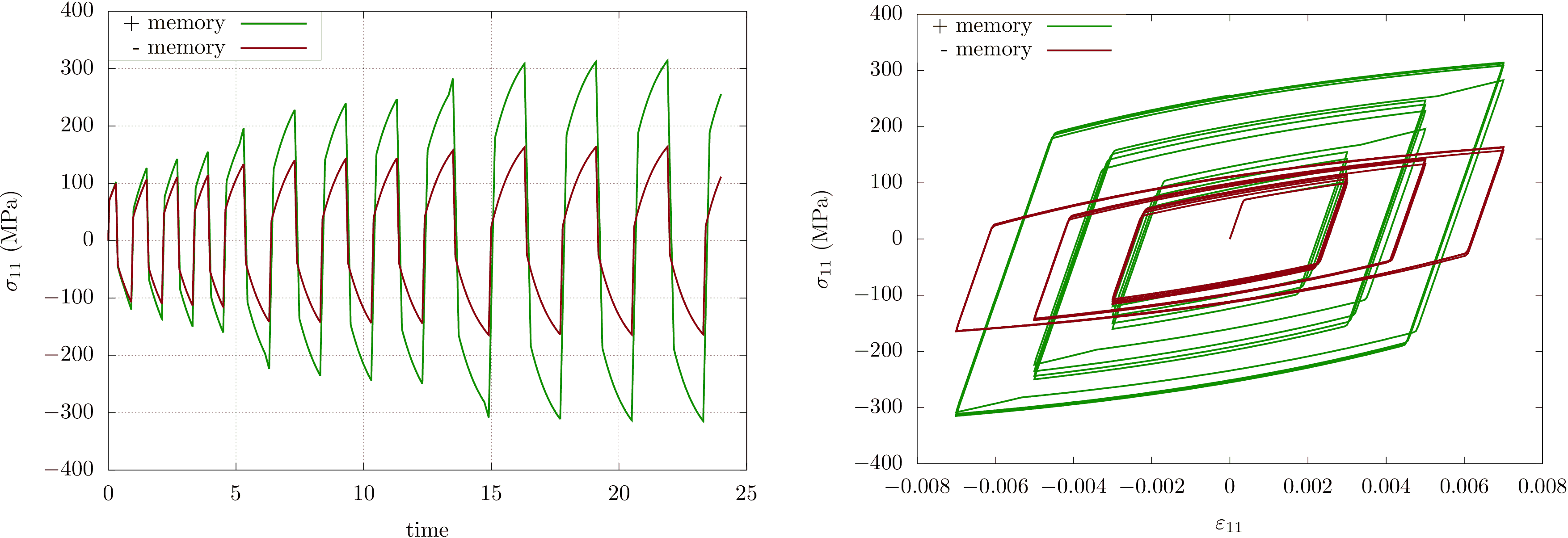
Fig. 12 A cyclic tension/compression loading with different strain amplitudes (4 cycles fo each amplitude) for models with and without memory.

Note

To describe strain range memory effect, one can also use nonlinear_with_memory isotropic hardening with gen_evp behavior as:

***behavior gen_evp
 **elasticity isotropic
   young 200000.
   poisson 0.3
 **potential gen_evp ev
  *flow norton
   n 5.
   K 50.
  *isotropic nonlinear_with_memory
   R0 50.0000
   b 25.0000
   Q0 25.0000
   Qsat 400.000
   mu 50.0000
  *kinematic nonlinear
   C 1000.00
   D 20.0000
  *kinematic nonlinear
   C 12000.00
   D 120.0000
 ***return