THERMAL_STRAIN

Description

This object is used to define the calculation of a volumetric thermal strain.

Syntax

The syntax for this object requires only input of the model coefficients (standard form). The types of thermal strain available are the following:

CODE	DESCRIPTION
isotropic	Isotropic thermal dilatation
anisotropic	Anisotropic thermal dilatation

The default type is isotropic.

The coefficients for the thermal strains are “secants.” That is to say that the thermal deformation \(\ten \varepsilon_{th}\) is given by the relation:

(484)\[{\epsilon_{th}}_i = \alpha_i(T,\dots) (T-T_{ref})\]

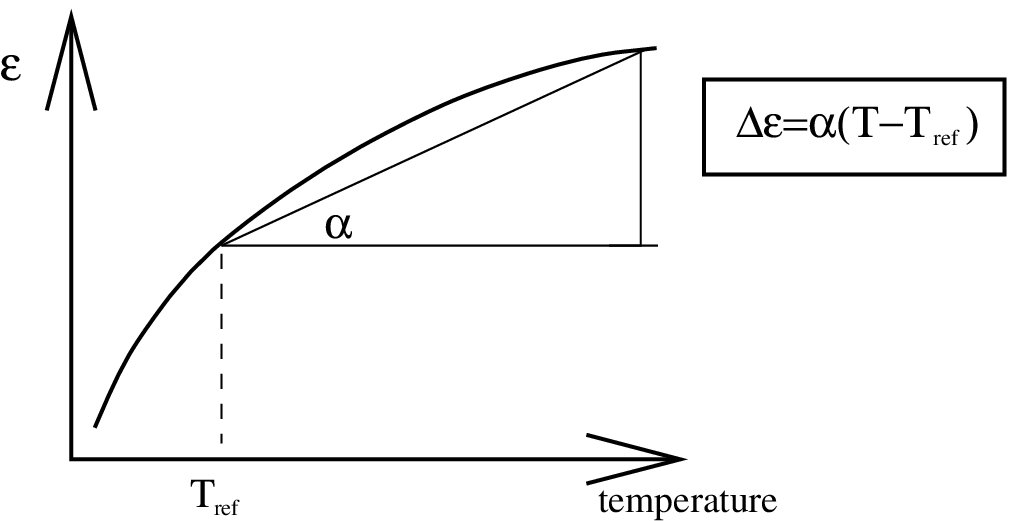
where \(\alpha_i(T,\dots)\) is the secant dilatation coefficient, \(T\) is the temperature, and \(T_{ref}\) is a reference temperature (zero by default).

Note

unexperienced users usually get confused about the exact signification of \(T_{ref}\). Let us consider, to clarify everything, the calculation of the incremental thermal strain at a given time \(t\) (it is assumed that the computation starts at \(t=0\) without thermal strain):

(485)\[\Delta\varepsilon^{0\rightarrow t}_{th}=\alpha(T(t))\left(T(t)-T_{ref}\right) - \alpha(T(t=0))\left( T(t=0)-T_{ref} \right)\]

In the previous equation, the dilatation coefficient \(\alpha(T)\) is supposed to be measured using \(T_{ref}\) as the reference temperature. Do not make any confusion between the initial time, which is the time at the beginning of the computation (usually \(t=0\)), and the reference temperature: \(T_{ref}\) is not related to any particular time; it is just the temperature used as ”reference“ by the people who did the experiment to measure \(\alpha\).

To re-define the reference temperature, a coefficient ref_temperature ^{1 1}a standard coefficient must be input. The method of calculation is schematically shown below:

The coefficients required for the thermal deformation models are given below. All coefficient types and dependencies may be entered for the thermal dilatation coefficients.

isotropic

The isotropic model has only one coefficient for the dilatational secant which is named alpha.

anisotropic

The anisotropic thermal strain object calculates different thermal strains along each axis in the material coordinate frame. The dilatational coefficients names are alpha1, alpha2, and alpha3 to the three material axes.

Example

**thermal_strain isotropic
  alpha     temperature
    10.e-6     25.
    12.e-6    500.
  ref_temperature 100.