**process manson_coffin#

Description#

This process computes the number of cycles to failure \(N_f\) according to Manson-Coffin fatigue model:

(20)#\[\begin{split} \begin{aligned} \dfrac{\Delta \ten \varepsilon}{2} & = \dfrac{\Delta \ten \varepsilon^p}{2} + \dfrac{\Delta \ten \varepsilon^e}{2} = \dfrac{\Delta \ten \varepsilon^p}{2} + \dfrac{\Delta \ten \sigma}{2E}\\ & = A N_f^{-\alpha}+BN_f^{-\beta} \end{aligned}\end{split}\]

  • \(A\) is the fatigue ductility coefficient.

  • \(-\alpha\) fatigue ductility exponent.

  • \(B = \dfrac{\sigma_f}{E}>0\), with \(\sigma_f\) is the fatigue strength coefficient, and \(E\) is the Young modulus.

  • \(-1\leq-\beta<0\) is the fatigue strength exponent.

For multi-axial loadings, the amplitudes of total, elastic and plastic strains are computed using the post-processing range.

  1. the elastic strain is computed from the input stress tensor and the Young modulus.

  2. the plastic strain can be either given by the user, or computed using a formula of type Ramberg–Osgood

    (21)#\[\dfrac{\Delta \varepsilon^p}{2} = A \left(\dfrac{1}{B}\dfrac{\Delta \varepsilon^e}{2}\right)^{\alpha/\beta}\]

  3. In case of elasticity, the coefficient \(A=0\).

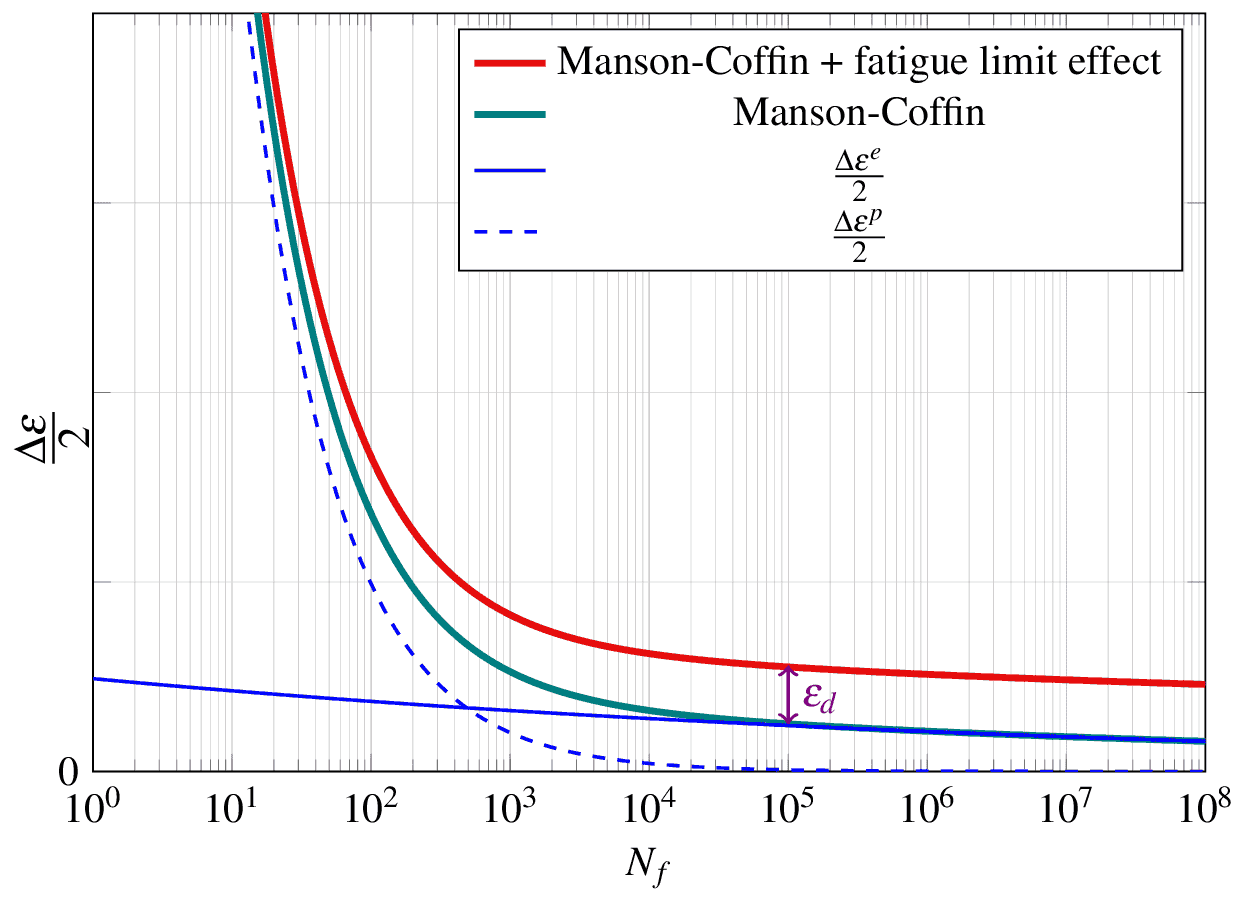
Fatigue limit effect#

It is considered by introducing a new parameter \(\epsilon_d\) in the fatigue model

\[\begin{aligned} \dfrac{\Delta \varepsilon}{2} & = \dfrac{\Delta \varepsilon^e}{2} + \dfrac{\Delta \varepsilon^p}{2} + \varepsilon_d \end{aligned}\]

such that \(N_f \longrightarrow \infty\) when \(\dfrac{\Delta \varepsilon}{2}<\varepsilon_d\). In this case, the eq. (21) becomes

(22)#\[\dfrac{\Delta \varepsilon^p}{2} = A \left[\dfrac{1}{B}\left(\dfrac{\Delta \varepsilon^e}{2}-\varepsilon_d\right)\right]^{\alpha/\beta}\]
../../_images/manson_coffin.png

Anisothermal case#

When the material parameters depends on the temperature, there is two ways to proceed:

  • Create a master curve with material parameters that are temperature-independent.

  • In some cases, no master curve can be drawn. In that case, this post-processing will try a find an equivalent temperature at which material parameters will be calculated. The model estimated at the equivalent temperature will provide an approximation of the fatigue model at different temperature. To estimate the equivalent temperature, an incremental damage model is used per cycle limited to only the elastic part of Manson-Coffin model.

    \[\dot D = \dfrac{1}{B\beta}\left<\dfrac{J(\ten \sigma-\overline{\ten\sigma})-E\varepsilon_D}{B}\right>^{\dfrac{1}{\beta}-1} J(\dot{\ten \sigma})\]

    where \(J(\ten \diamond) = \sqrt{\dfrac{2}{3}\ten \diamond^{dev}:\ten \diamond^{dev}}\) This incremental model is integrated using either Newton-Raphson algorithm or dichotomy. If a temperature is not found then the equivalent temperature is set to the most damaging temperature from minimum and maximum temperatures.

Syntax#

**process manson_coffin \(~\,\) *var stress [ *plastic ein ] [ *infinity_is infinity ] [ *precision epsilon ] [ *iteration iter ] [ *full_output ] [ *for_cumulation ] [ *max_dT dT_max ]

*var stress

the name of the stress tensor

*plastic ein

the name of the plastic strain variable. If ein = cyclic_hardening, then the amplitude of plastic strain increment is estimated using (22). If this option is not specified, only the elastic part of the model will considered (i.e., \(A=0\)).

*infinity_is infinity

a value for the number of cycles to failure, \(N_f\), that should be treated as infinite. By default 1e15.

*precision epsilon

precision value required for solving (20) either by Newton-Raphson or dichotomy algorithms. By default 1e-4.

*iteration iter

The maximum number of iterations for algorithms used to integrate. By default 500.

*full_output

a flag to output amplitudes of elastic and plastic strains. By default false.

*for_cumulation

a flag to output the cumulated damage.

*max_dT dT_max

maximum temperature increment \(\Delta T\). By default 10.

Example#

****post_processing
 ***local_post_processing
  **material_file manson.data
  **file integ
  **elset ALL_ELEMENT
  **process manson_coffin
   *var sig
   *plastic evi
   *full_output
   *for_cumulation
****return

where

 % manson.data
***post_processing_data
 **process manson_coffin
   young temperature
   119000.   0.
   100000.    300.
   alpha  temperature
   0.85       0.
   0.7        300.
   A      temperature
   1.055      0.
   0.7797     200.
   1.1085     300.
   beta temperature
   0.1133   0.
   0.0655   300.
   B temperature
   0.012411   0.
   0.007272  300.
   epsd    temperature
   0.001428   0.
   0.001552   200.
   0.001360   300.
***return